미분방정식 알아 보기

1. 미분 독립변수 x가 연속적으로 변함에 따라 종속변수 y도 연속적으로 변할 때 어느 한 점에서 종속변수 변화량 Δx와 독립변수 변화량 Δy의 비율의 극한을 그 점에서의 ‘미분계수’ 또는 ‘순간변화율’이라고 합니다.

이에 비해 단순히 종속변수 변화량 Δx 와 독립변수 변화량 Δy의 비율을 평균변화율이라 하죠. 1-1. 평균변화율 x가 a로부터 a+Δx인 b로 변화될 때 함수 f(x)의 평균 변화율은 다음과 같습니다.

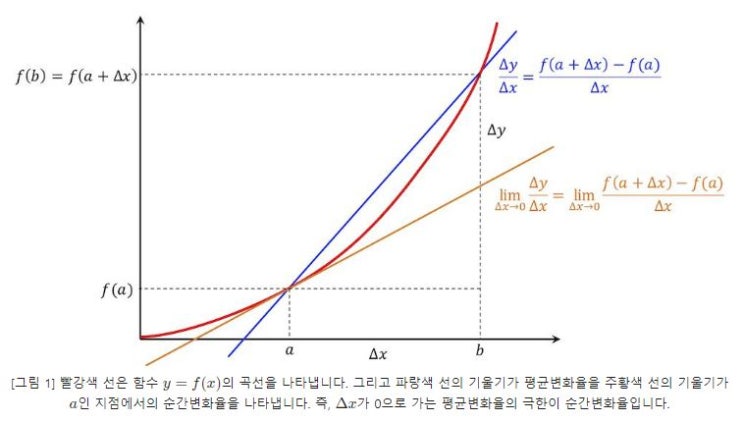
아래 [그림 1]에서 파랑색 직선의 기울기가 평균변화율을 뜻합니다. 1-2. 순간변화율 (미분계수) (1)식에서 Δx→0일 때의 극한값이 순간변화율입니다.

수학적으로 표현하면 아래 식과 같습니다. 이때 (2)식은 너무 길어 평소에 사용하기 불편하잖아요.

이를 줄여서 다음과 같이 표현합니다. 읽을때는 x = a지점에서의 순간변화율 (또는 미분계수, 또는 기울기)이라고 합니다.

무엇을 사용하든 다 똑같은 의미에요. [그림 1]에서 주황색 직선의 기울기가 a인 지점에서의 순...